(As usual, all code and notebooks are available at https://github.com/csdurfee/hot_hand)
Last time, we saw that LeBron James was by far the un-streakiest player in the NBA over the last 20 years and found out that it's at least partly caused by shot selection. He takes both lower percentage shots than average when he's shooting well and higher percentage shots than average when he's shooting poorly.
LeMartingale
I got the question of why it's OK to use a player's overall FG% to gauge their streakiness. We know that every shot a player takes has a slightly different level of difficulty, and thus a different probability that it will go in. Shouldn't that affect the streakiness?
It's a good question. Let's say you've got a bag with 2 types of coins inside. One of them comes up heads 40% of the time, the other comes up heads 60% of the time. You can't tell which is which. If you pick a coin randomly out of the bag and flip it, what are the chances, on average, it comes up heads?
It's 50%, right? The selecting of the coin and the flipping of the coin are two independent steps. We can multiply the probabilities at each step together, so the overall chances of heads are (.5 * .4) + (.5 * .6) = .5. If we kept randomly selecting from the bag and flipping a coin, the results would be indistinguishable from just flipping a single fair coin over and over.
In math, this is known as a Martingale. Previous outcomes don't give us information about the next event. (More in depth explanation here). That's different from LeBron. We know he essentially chooses the 60% heads coin when he's been getting a lot of tails recently, and the 60% tails coin when he's been getting a lot of heads recently.
LeSimulation
If I create a simulation of LeBron James that uses his exact shooting tendencies and FG percentages, and the shot selection is totally random, it shouldn't show any streaky or unstreaky tendencies beyond expected by chance. Let's see what LeSimulation looks like.
At the end of the last edition, I got LeBron's shooting stats:
Above the Break 3 0.344598
Backcourt 0.058824
In The Paint (Non-RA) 0.401369
Left Corner 3 0.394799
Mid-Range 0.379890
Restricted Area 0.720138
Right Corner 3 0.370370
And shooting tendencies (what percent of the time he takes each type of shot):
Above the Break 3 0.204940
Backcourt 0.001160
In The Paint (Non-RA) 0.109652
Left Corner 3 0.014431
Mid-Range 0.267715
Restricted Area 0.386442
Right Corner 3 0.015660
The simulation randomly chooses a shot type, based on the actual tendencies, then attempts a shot at the corresponding FG%.
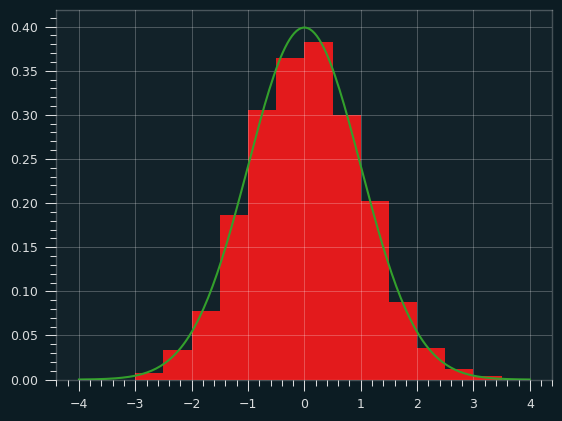
The z-scores look like they should -- mean is very close to 0, standard deviation close to 1. No streaky/unstreaky tendencies, as promised. No evidence that shot attempts were at different FG%.
LeSimulation 2 - last 5 FG%
My next simulation uses LeBron's FG% over his last 5 shots. We've seen he shoots the best with 0 makes in his last 5; the worst with 5 makes in his last 5. The simulation uses his exact percentages at each level. For the first 5 shots of every game, it uses his career FG%.
I ran the simulation 1,000 times. Here are the z-scores:
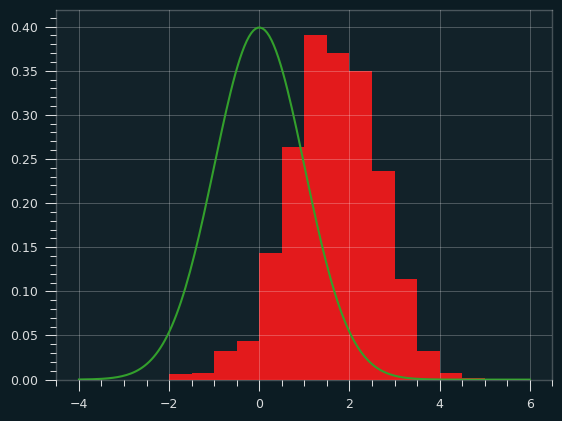
As expected, this simulation is pretty un-streaky:
count 1000.000000
mean 1.635843
std 0.985464
min -1.665389
25% 1.001550
50% 1.623242
75% 2.346864
max 4.509869
It's still not nearly as unstreaky as the man himself, though -- Lebron's z score of 5.9 would be way bigger than the largest value in 1,000 simulations (4.5). So he'd still be an outlier compared to these simulated un-streaky players.
LeSimulation 3 -- No resetting streaks
What about a fake player where the streaks don't reset between games? That should make the simulated player even more unstreaky.
In this version of the simulation, every shot will be influenced by the FG% of the previous 5 shots, even if they happened in the previous game(s).
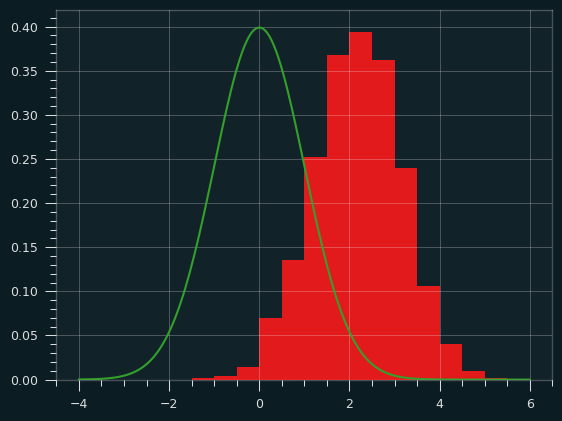
Here are the corresponding z-scores:
count 1000.000000
mean 2.179821
std 0.963330
min -1.033468
25% 1.536542
50% 2.203681
75% 2.865350
max 5.073167
So, the mean went from 1.6 to 2.2, and the max z score went from 4.5 to 5.1. That's still not nearly unstreaky enough to match LeReal LeBron, but at least it's closer.
It's possible that if we tracked the last 7 shots, or 9, instead of 5, we would see even more of a dramatic change in FG percentage. Or there's some other factor I haven't considered that is adding unstreakiness, such as the fact that his FG percentage tends to go down the more shots he's taken in a game.
DoppLeGangers
I was curious if I could find similar players to LeBron. There's a good way to do that, but I wanted to try my own way first. I found players where, like LeBron, their FG% steadily declines the more shots they've made out of the last 5. There are 18 such players: Karl Malone, Grant Hill, Ben Wallace, Eddie House, Michael Redd, Jarvis Hayes, Andres Nocioni, JJ Redick, Nicolas Batum, Goran Dragic, DeMar DeRozan, Patrick Beverley, Marcus Morris Sr., Bradley Beal, Kelly Oubre Jr., Norman Powell, Donte DiVincenzo, and Landry Shamet.
Overall, these players have a mean z-score of 1.47, which is pretty impressive, but except for Goran Dragic, there isn't much overlap over the players with the highest overall z scores. 18 players is a pretty small sample size, as well.
I also looked at a broader set of players where at least 4 out of the 5 comparisons were decreasing. This gave 180 players, with an average z score of 1.0.
LeRight way
The right way to identify LeBron-alikes is to use a similarity metric that I didn't invent. The fg percentages after 0..5/5 makes are sort of like a probability distribution. There's a lot of work in statistics and machine learning around comparing distributions -- could this data come from this distribution? Is it a good representation of the observed data? A common tool to use is relative entropy, also known as KL divergence.
If we normalize the shooting percentages and compare them to LeBron's, players with a low relative entropy should show the same tendency to shoot better when they're shooting worse than average over their last 5, and vice versa.
For example, LeBron's last 5 percentages are:
0 0.564612
1 0.50712
2 0.505937
3 0.496538
4 0.473849
5 0.464052
By normalizing them, they look like a probability distribution (they all add up to one) but it still has the same shape as the raw values if we made a bar chart.
0 0.187448
1 0.16836
2 0.167968
3 0.164847
4 0.157315
5 0.154062
The normalization also corrects for the fact that some shooters have higher FG% overall than other players.
Normalized values can then be compared to other players' values. The lower the entropy, the more similar their shapes are.
I also calculated the Jensen-Shannon distance, which is like relative entropy, but symmetrical (distance(le_bron, le_other_guy) = distance(le_other_guy, le_bron)).
The closest guys to LeBron by this measure are CJ McCollum, Terry Rozier, Andrea Bargnani, Marcus Morris, Richard Hamilton, Nikola Vucevic, Zach Randolph, Lauri Markkanen, Kawhi Leonard, and Kevin Huerter.
Since Richard Hamilton had the streakiest game in the last 20 years, it's not surpring to see him. But except for Randolph and Vucevic, none of the top 10 had exceptional z scores, though they were all positive.
The Jensen-Shannon distance results were extremely similar to entropy. It agreed exactly with the entropy as far as ordering 73 of the top 100 players. The average z score for those players was 1.16, versus 1.15 for entropy. So, in aggregate, both were better than my homegrown metric at identifying unstreaky players.
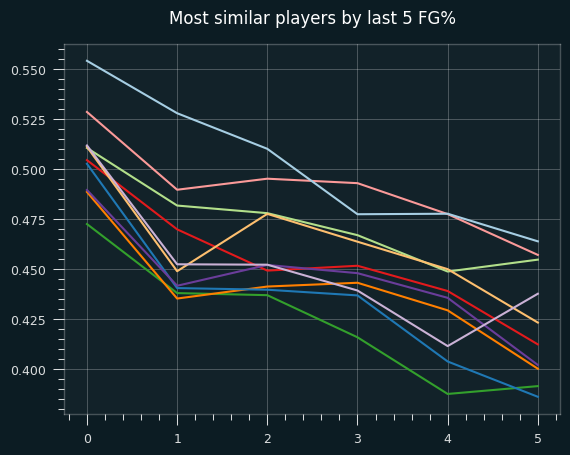
I haven't looked at whether the reason for the trend in last 5 FG% is due to shot selection for these other players, which is probably the interesting part. Some of the players flagged here are inevitably due to chance. It's based on five 50/50 measurements, so 1 in 32 players would get flagged as "LeBron like" even if the data was randomly generated.
None of my queries here turned up the un-streakiest players like Luka Doncic and Anthony Edwards. Whatever causes their extreme unstreakiness (beyond randomness) must be different from LeBron's tendencies. Stay tuned!